Masked Grid for Two Sides of a Fault

In this example, I demonstrate how to use a surface mesh of a fault in the subsurface to create a data mask on a modeling grid. This is a particularly useful exercise for scenarios where you may want to perform some sort of modeling in a different manner due to geological differences on the two sides of the fault - but still have a single modeling grid.

Let’s get to it!

# sphinx_gallery_thumbnail_number = 4
import numpy as np
import pooch
import pyvista as pv

url = "https://raw.githubusercontent.com/pyvista/vtk-data/master/Data/opal_mound_fault.vtk"
file_path = pooch.retrieve(url=url, known_hash=None)
fault = pv.read(file_path)
fault

PolyData	Information
N Cells	3834
N Points	2029
N Strips	0
X Bounds	3.361e+05, 3.389e+05
Y Bounds	4.258e+06, 4.264e+06
Z Bounds	-2.606e+03, 2.906e+03
N Arrays	0

Create the modelling grid if you don’t already have one

grid = pv.UniformGrid()
# Bottom south-west corner
grid.origin = (329700, 4252600, -2700)
# Cell sizes
grid.spacing = (500, 500, 500)
# Number of cells in each direction
grid.dimensions = (30, 35, 10)
grid

/opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages/pyvista/core/grid.py:912: PyVistaDeprecationWarning: `UniformGrid` is deprecated. Use `ImageData` instead.
  warnings.warn(

UniformGrid	Information
N Cells	8874
N Points	10500
X Bounds	3.297e+05, 3.442e+05
Y Bounds	4.253e+06, 4.270e+06
Z Bounds	-2.700e+03, 1.800e+03
Dimensions	30, 35, 10
Spacing	5.000e+02, 5.000e+02, 5.000e+02
N Arrays	0

Take a quick preview to see where the fault is inside of the grid

p = pv.Plotter()
p.add_mesh(grid, opacity=0.5)
p.add_mesh(fault, color="orange")
p.show()

You may notice that the modeling grid’s extent is far greater than that of the fault – not to worry! PyVista’s clip_surface filter and the utility I’m going to share below handles this quite well by interpolating the fault’s plane outward.

This is a reusable utility for performing the mask:

def mask_mesh_by_surface(mesh, surface):
    grid = mesh.copy()
    # Split the mesh by the fault
    grid["pids"] = np.arange(grid.n_points)
    grid["cids"] = np.arange(grid.n_cells)
    a = grid.clip_surface(surface, invert=False, compute_distance=True)
    b = grid.clip_surface(surface, invert=True, compute_distance=True)
    # Inject the mask
    grid["cell_mask"] = np.zeros(grid.n_cells, dtype=int)
    grid["cell_mask"][a["cids"]] = 1
    grid["cell_mask"][b["cids"]] = 2
    # Use implicit distance to get point mask
    lpids = np.argwhere(grid["implicit_distance"] >= 0)
    gpids = np.argwhere(grid["implicit_distance"] < 0)
    grid["point_mask"] = np.zeros(grid.n_points, dtype=int)
    grid["point_mask"][lpids] = 1
    grid["point_mask"][gpids] = 2
    return grid

Let’s run it and take a look at the result!

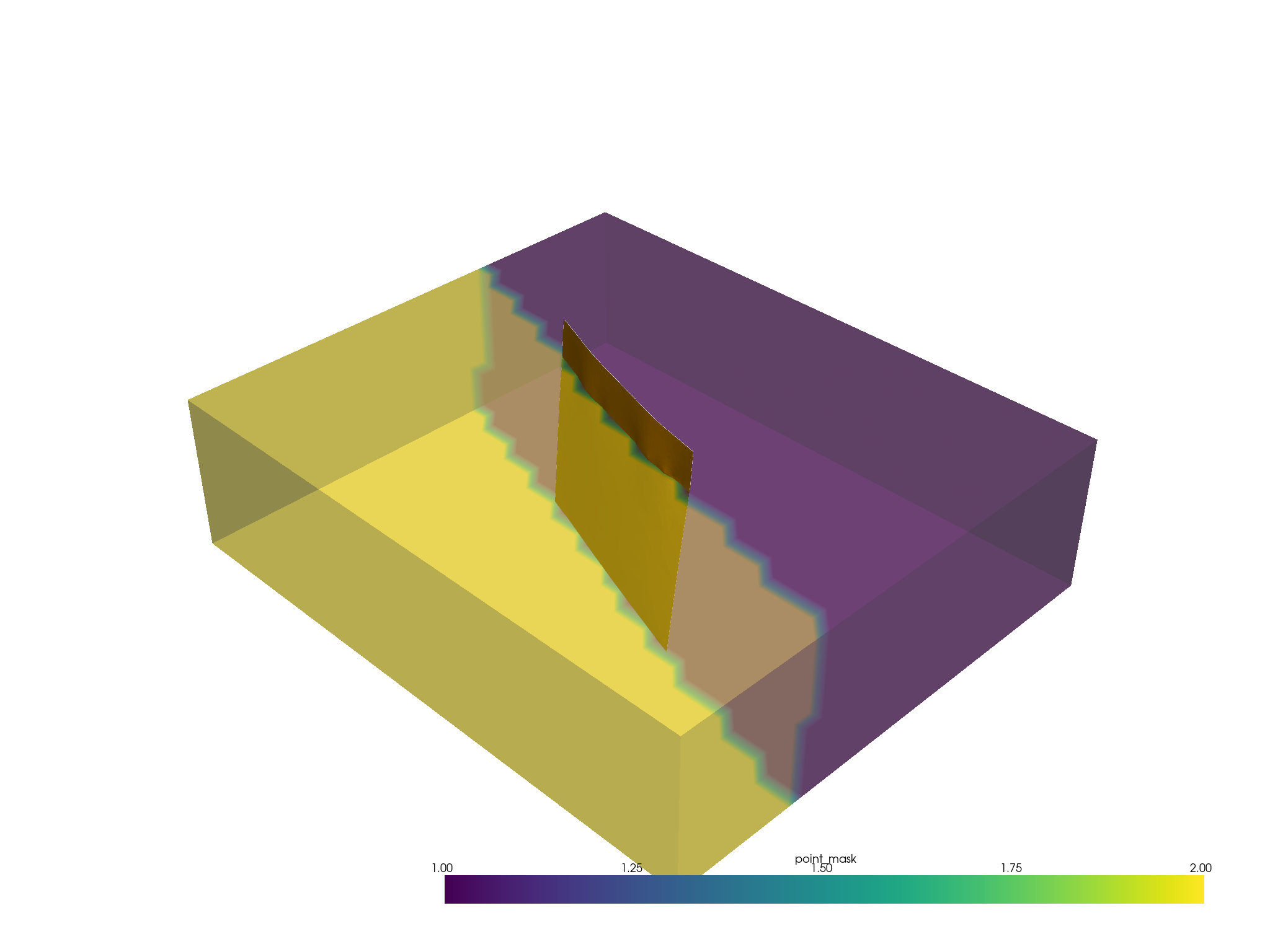
masked = mask_mesh_by_surface(grid, fault)

p = pv.Plotter()
p.add_mesh(fault, color="orange")
p.add_mesh(masked, scalars="point_mask", opacity=0.5)
p.show()

/opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages/pyvista/core/grid.py:912: PyVistaDeprecationWarning: `UniformGrid` is deprecated. Use `ImageData` instead.
  warnings.warn(

And here is how you might use that mask to do some sort of fancy modeling. In my example, I’m going to use a rather sophisticated distance calculation:

ids = np.argwhere(masked["point_mask"] == 1).ravel()
pts = grid.points[ids]
len(pts)

5659

Compute distance from TNE corner

compute = lambda a, b: np.sqrt(np.sum((b - a) ** 2, axis=1))
dist = compute(pts, np.repeat([masked.bounds[1::2]], pts.shape[0], axis=0))

Add those results back to the source grid

masked["cool_math"] = np.zeros(grid.n_points)  # Need to preallocate
masked["cool_math"][ids] = dist

# Do some different math for the other side
...

Ellipsis

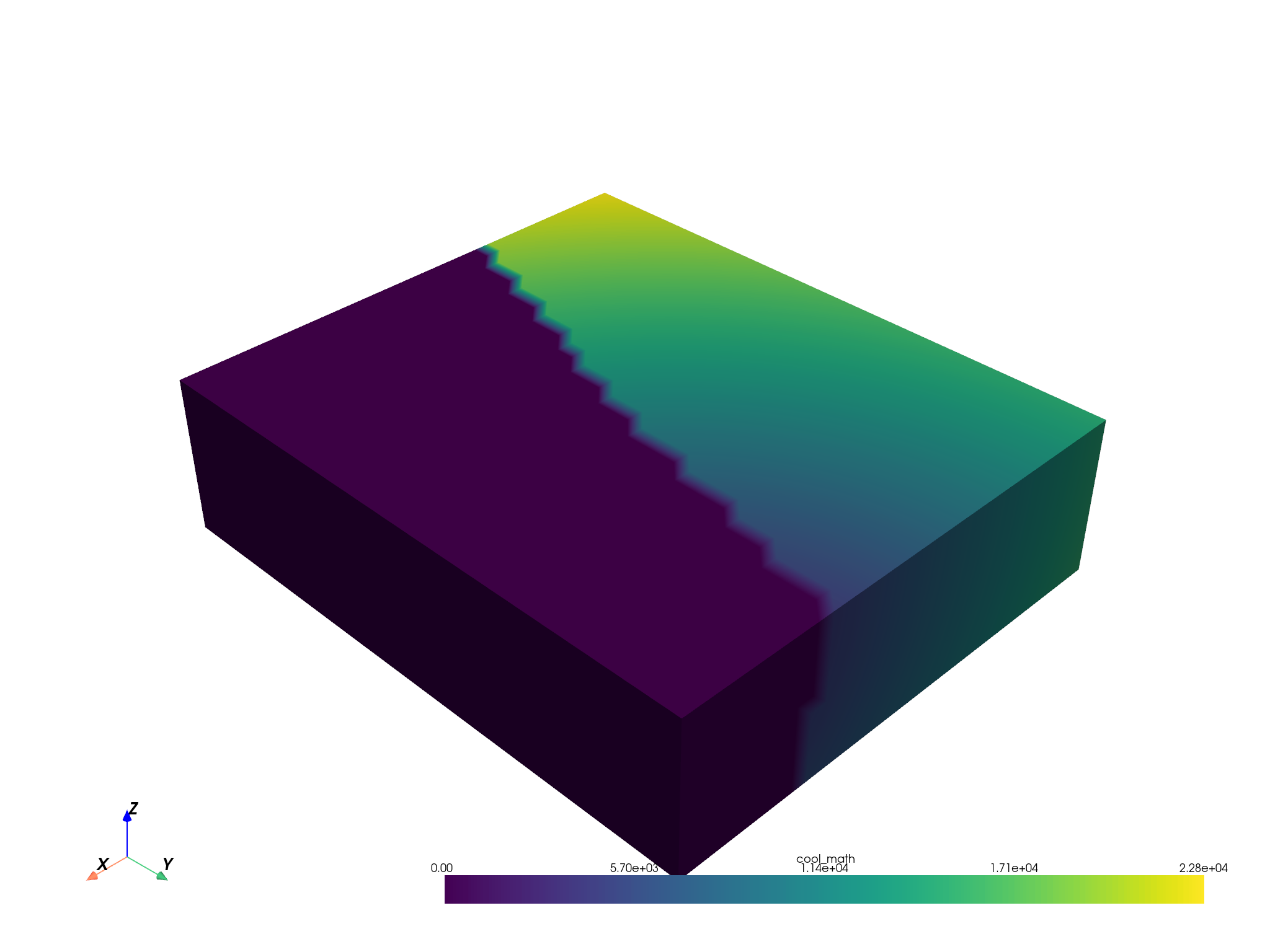
Display!

masked.plot(scalars="cool_math")

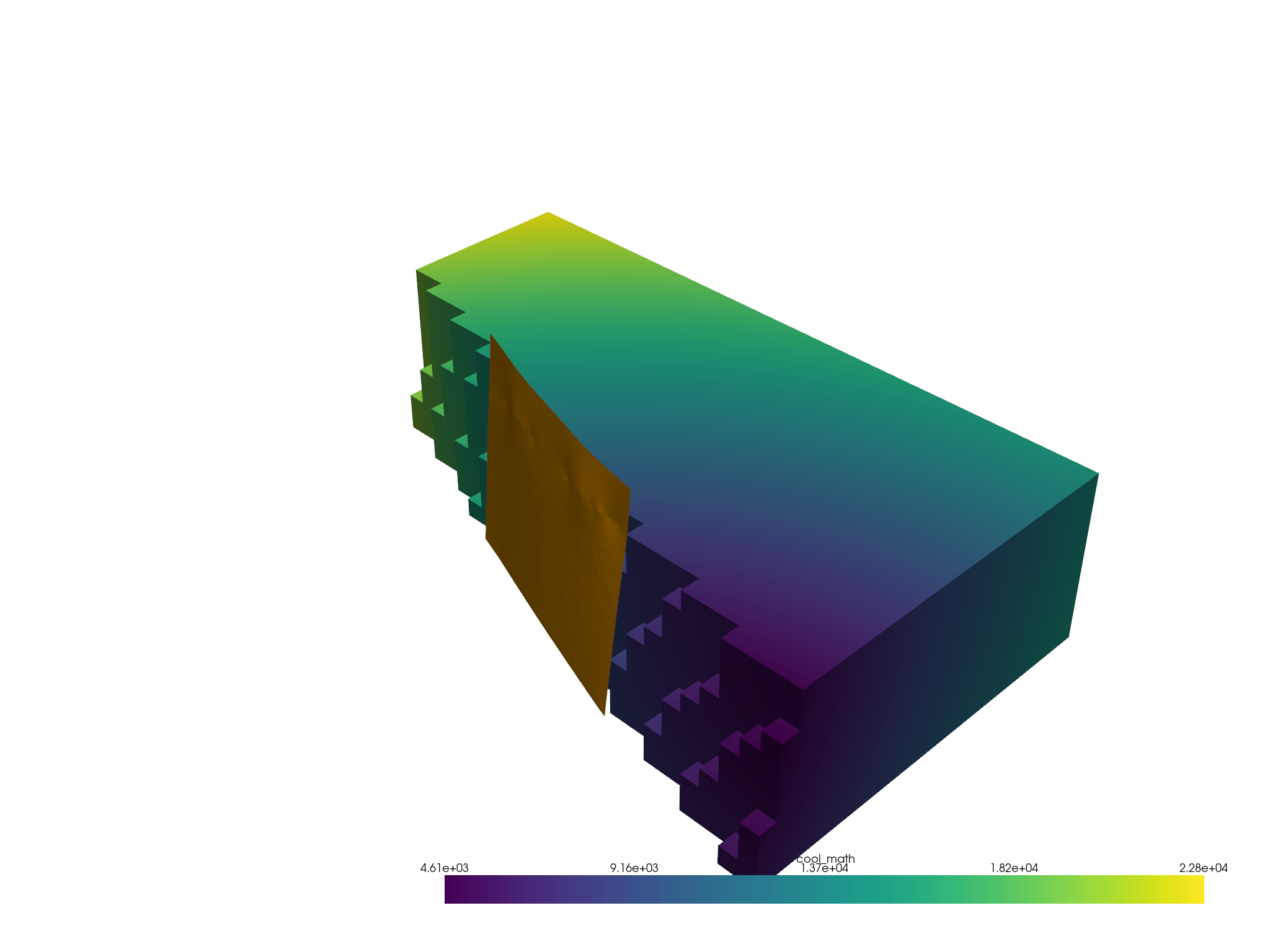
Visualize one side of the masked grid

a = masked.threshold(1.5, scalars="cell_mask", invert=True)

p = pv.Plotter()
p.add_mesh(a, scalars="cool_math")
p.add_mesh(fault, color="orange")
p.show()